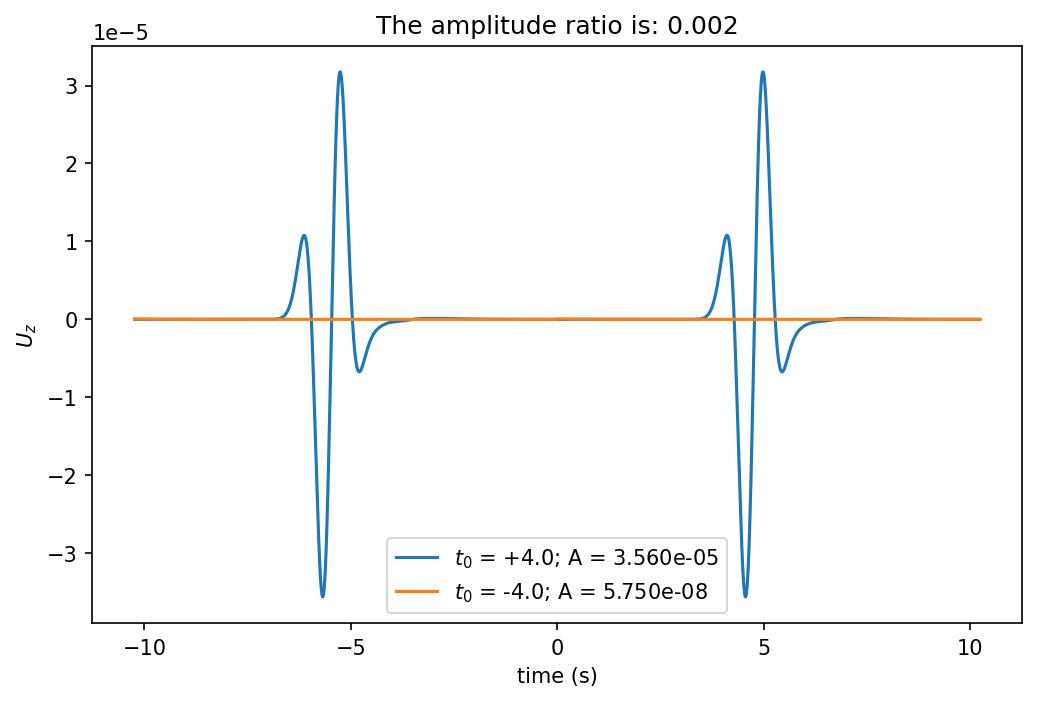
不合适的时移参数
当震源子波的时移参数 $ t_0 $ 不合适时,GRTM 计算出的波形会分裂出现在记录时窗的两端:
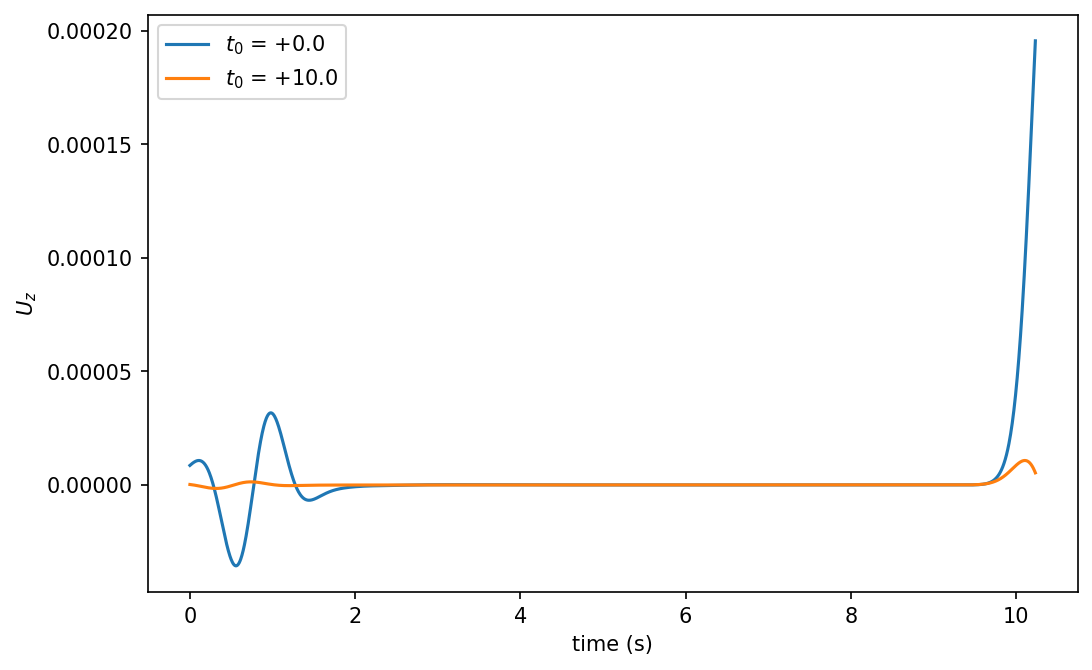
实际上,无论 $ t_0 $ 取值如何,波形始终都是“分裂”的,首端和末端的波形振幅放大倍数是不一致的,时窗起点和终点的幅值是不一样的。只是当 $ t_0 $ 取在记录时窗的中部时,两端波形的实际幅值趋于 0,不同的振幅放大倍数的作用效果并不明显。
可以验证的是,$ t_0 = 0 $ 时的首端振幅放大倍数与 $ 0 < t_0 < T $ 时的倍数一致,尾端则与 $ - T < t_0 < 0 $ 时一致(这里,$ T $ 表示总的记录长度):
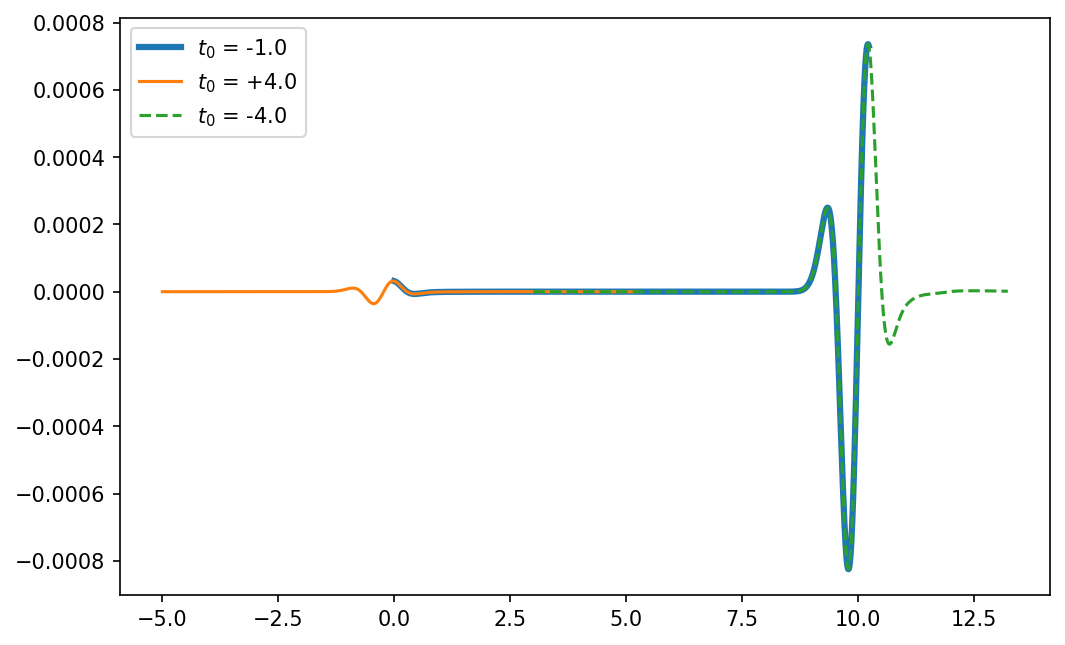
注:为了方便比较波形,这里对 $ t_0 = \pm 4.0 $ 时的波形分别做了额外的时移。
在记录时长和时间步长保持不变时
从上图中可以发现,由不同时窗区间 $ U_i = \big[ (i - 1) \cdot T, i \cdot T \big] $(当 $ i = …, -1, 0, 1, … $ 时)内取值的 $ t_0 $ 计算出的波形的振幅存在差异:
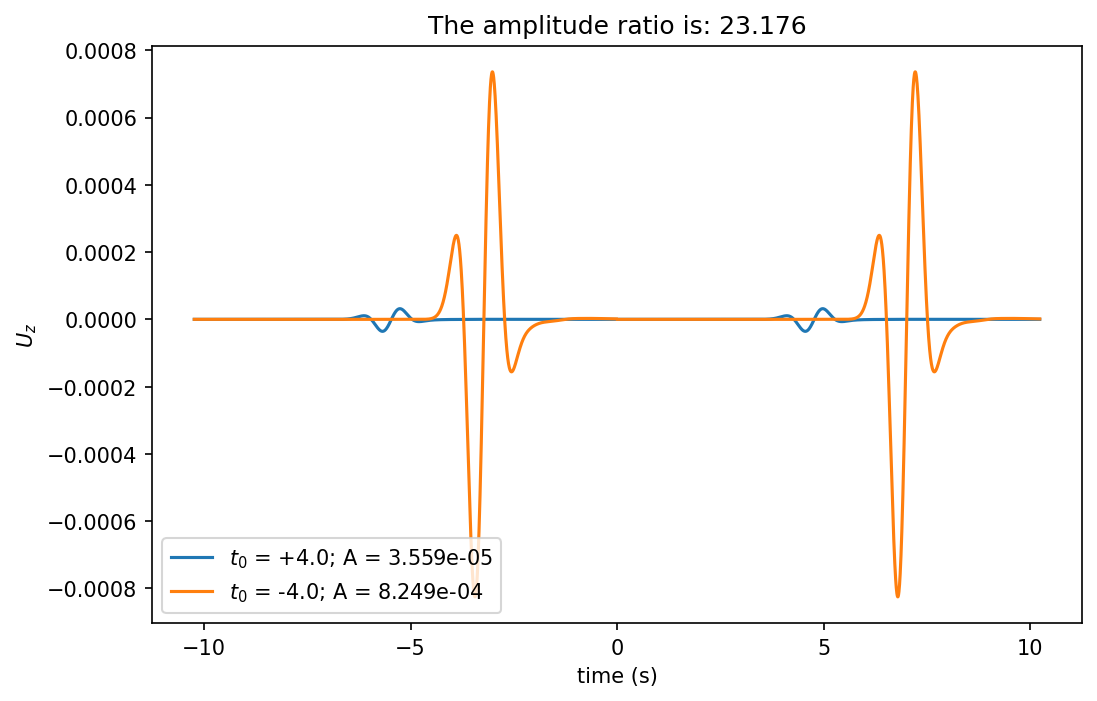
注:为了方便比较可能存在的分裂两端的波形,这里对计算出的波形在负时间轴做了周期扩展。
当进一步向负轴取相邻区间的不同 $ t_0 $ 时,波形的振幅比不会发生变化:
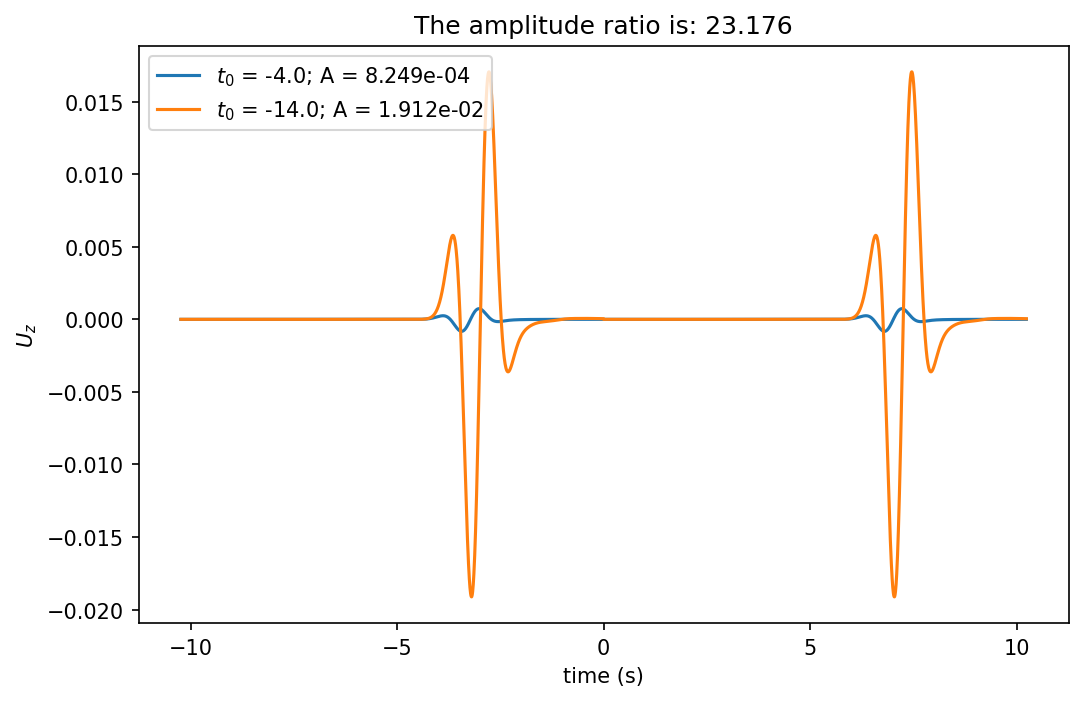
而由同一区间内的不同 $ t_0 $ 计算出的波形振幅相同:
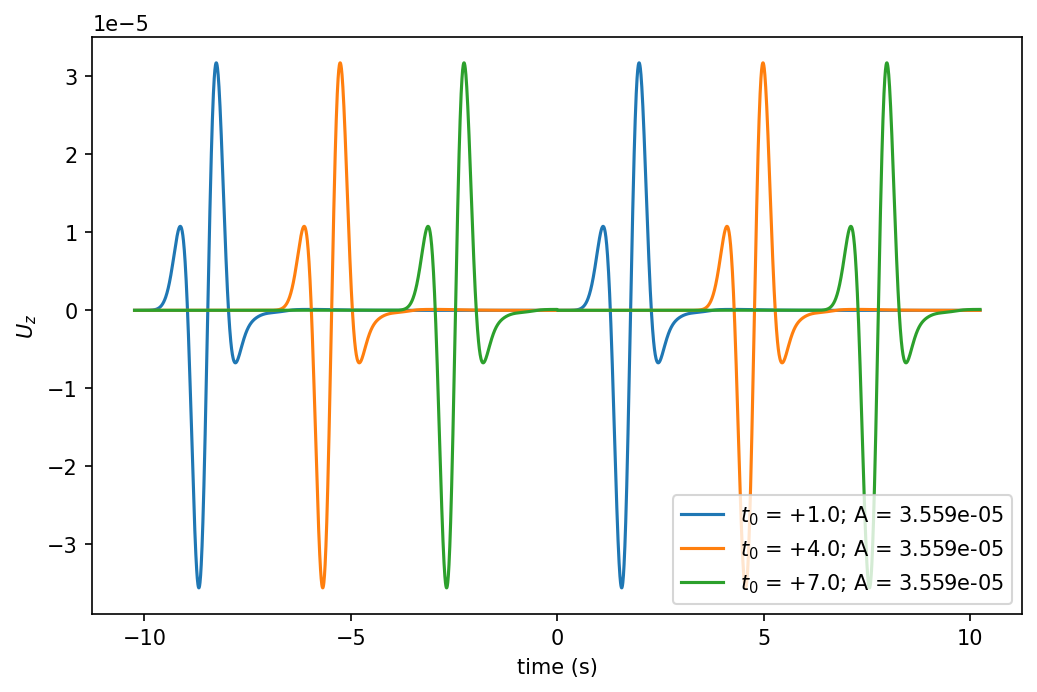
在记录时长发生变化时
从前图中可以发现,向后时移(在 $ U_i $ 区间)计算出的波形振幅比向前时移(在 $ U_j $ 区间,且 $ j > i $)的大。但这一点不是恒成立的。当取不同的记录长度时,波形的振幅比可能发生变化:
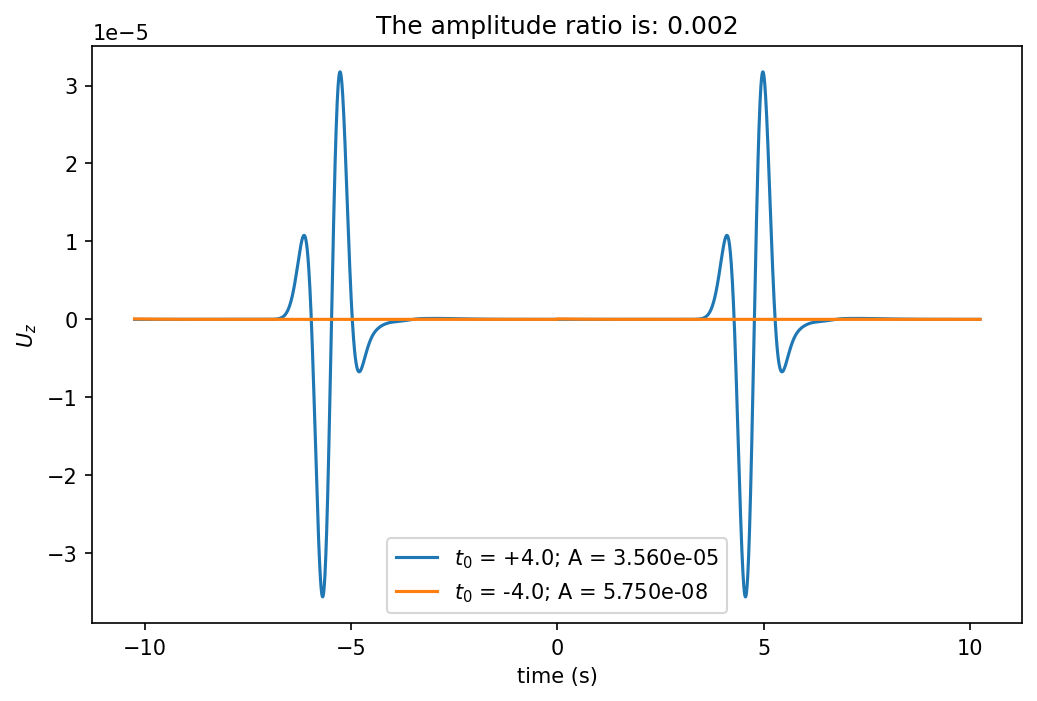
在时间步长发生变化时
同样地,当取不同的时间步长时,波形的振幅比也可能发生变化: